Machine Learning in der Pflege
Machine Learning (ML) ist eine Teilmenge der künstlichen Intelligenz (KI), die es Computern ermöglicht, aus Daten zu lernen und Vorhersagen zu treffen oder Entscheidungen zu treffen, ohne explizit programmiert zu sein. Im Gegensatz zur Nutzung von Sprachmodellen, die auf großen Textdatensätzen trainiert werden, um natürliche Sprache zu verstehen und zu erzeugen, konzentriert sich Machine Learning darauf, Muster in numerischen oder kategorischen Daten zu erkennen.
Unterschiede zur Nutzung von Sprachmodellen
- Sprachmodelle: Verwendet für Textverarbeitung, Übersetzungen, Sprachgenerierung und -verstehen. Sie basieren oft auf großen Datensätzen und komplexen Architekturen wie neuronalen Netzwerken.
- Machine Learning: Weitreichender Anwendungsbereich, der von einfachen linearen Regressionen bis hin zu komplexen Deep Learning-Modellen reicht. Es wird verwendet, um Muster in Daten zu erkennen und Vorhersagen zu treffen, die in vielen Branchen angewendet werden können.
Anwendungen von Machine Learning
- Vorhersagemodelle: Vorhersage von zukünftigen Ereignissen auf Basis historischer Daten, wie z.B. Wettervorhersagen, Aktienkurse oder Verkaufsprognosen.
- Klassifikation: Einordnung von Daten in Kategorien, wie z.B. Spam-Erkennung in E-Mails oder Diagnose von Krankheiten.
- Clustering: Gruppierung von Datenpunkten, um Muster oder Ähnlichkeiten zu erkennen, z.B. in der Kundensegmentierung.
- Anomalieerkennung: Identifikation von ungewöhnlichen Datenpunkten, die von der Norm abweichen, z.B. in der Betrugserkennung.
In der Pflege kann Machine Learning verwendet werden, um die Qualität der Betreuung zu verbessern, indem es Muster in Patientendaten erkennt, die Effizienz von Pflegeprozessen optimiert und die Entscheidungsfindung unterstützt.
Datenvorbereitung im Machine Learning
Der größte Teil der Arbeit im Machine Learning besteht in der Auswahl und Vorbereitung der Daten. Dies umfasst:
- Datensammlung: Zusammenstellen relevanter Daten aus verschiedenen Quellen.
- Datenbereinigung: Entfernen von Fehlern oder Ungenauigkeiten in den Daten.
- Feature-Engineering: Erstellen neuer relevanter Merkmale aus bestehenden Daten.
- Datenaufteilung: Aufteilen der Daten in Trainings- und Testsets zur Modellbewertung.
Einfache lineare Regression
In diesem Beispiel verwenden wir eine einfache lineare Regression, um die Beziehung zwischen Personalkosten und der Anzahl der verordneten Psychopharmaka zu modellieren. Dies ist eine der grundlegendsten Techniken im Machine Learning, aber es ermöglicht uns, die grundlegenden Konzepte zu verstehen. Natürlich kann Machine Learning auch viel komplexere Zusammenhänge und Modelle darstellen, um tiefere Einblicke zu gewinnen.
Sie sehen gerade einen Platzhalterinhalt von YouTube. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Einfache Lineare Regression für Pflegeheim-Daten
Dieses Repository enthält ein Beispiel für eine einfache lineare Regression, die Beispiel-Daten für eine Träger von mehreren Pflegeeinrichtungen verwendet, um die Beziehung zwischen Personalkosten und der Anzahl der verordneten Psychopharmaka zu modellieren. Jede Reihe stellt eine Stationseinheit mit z.B. 30 Bewohnern dar und die zweite Spalte die Anzahl der verordneten Psychopharmaka aller Bewohner. Ich stelle einfach einen Zusammenhang (Korrelation) dar: Je mehr oder qualifizierter das Personal, desto weniger Psychopharmaka benötigt man. Ob es wirklich so einen Zusammenhang gibt, keine Ahnung, ich glaube so eine Studie will keiner.
Schritt 1: Laden des Datensatzes
Zuerst laden wir den Datensatz und definieren die unabhängige und abhängige Variable. Der Datensatz enthält zwei Spalten: die jährlichen Personalkosten und die Anzahl der verordneten Psychopharmaka.
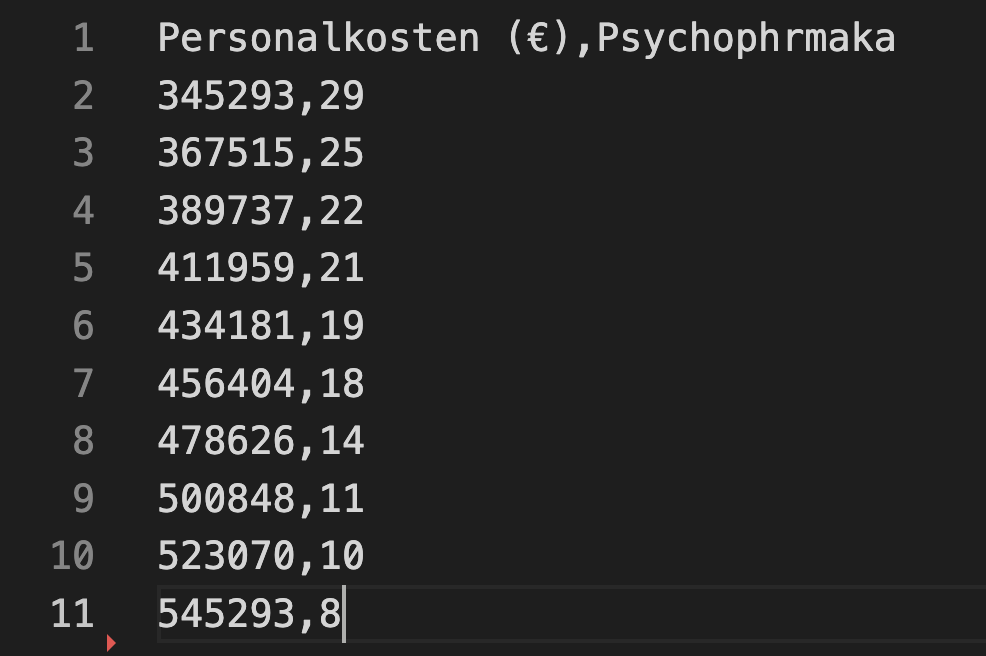
Das ist eine csv-Datei jede Spalte Reihe ist durch ein Komma getrennt.
import pandas as pd
# Laden des Datensatzes
dataset = pd.read_csv('Data/drugs_nursing_home.csv')
X = dataset.iloc[:, :-1].values # Unabhängige Variable (Personalkosten)
y = dataset.iloc[:, -1].values # Abhängige Variable (Psychopharmaka)Erklärung: Hier verwenden wir die pandas-Bibliothek, um den Datensatz zu laden. X repräsentiert die Personalkosten (unabhängige Variable) und y die Anzahl der verordneten Psychopharmaka (abhängige Variable).
Schritt 2: Aufteilen des Datensatzes
Um die Modellleistung zu bewerten, teilen wir den Datensatz in Trainings- und Testdaten auf.
from sklearn.model_selection import train_test_split
# Aufteilen des Datensatzes in Trainings- und Testdaten
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)Erklärung: Der Datensatz wird mit train_test_split aus der scikit-learn-Bibliothek in 80% Trainingsdaten und 20% Testdaten aufgeteilt. Der Parameter random_state=0 stellt sicher, dass die Aufteilung reproduzierbar ist.
Schritt 3: Trainieren des Modells
Nun trainieren wir das lineare Regressionsmodell mit den Trainingsdaten.
from sklearn.linear_model import LinearRegression
# Trainieren des Modells
regressor = LinearRegression()
regressor.fit(X_train, y_train)Erklärung: Wir erstellen ein LinearRegression-Objekt und trainieren es mit den Trainingsdaten. Das Modell lernt, die Beziehung zwischen Personalkosten und der Anzahl der verordneten Psychopharmaka zu erkennen.
Schritt 4: Visualisierung der Trainingsdaten
Wir visualisieren die Ergebnisse des Trainings, um zu sehen, wie gut das Modell die Trainingsdaten erfasst.
import matplotlib.pyplot as plt
# Visualisierung der Trainingsdaten
plt.scatter(X_train, y_train, color='green')
plt.plot(X_train, regressor.predict(X_train), color='blue')
plt.title('Personalkosten vs Psychopharmaka (Training set)')
plt.xlabel('Personalkosten im Jahr')
plt.ylabel('Psychopharmaka')
plt.show()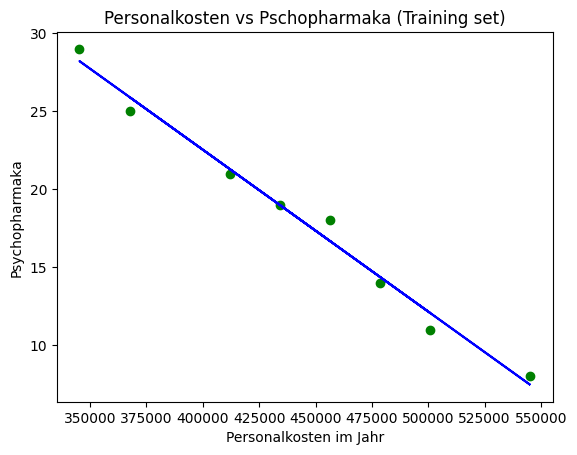
Erklärung: Das Streudiagramm zeigt die tatsächlichen Trainingsdaten (grüne Punkte), während die blaue Linie die vom Modell vorhergesagten Werte darstellt. Dies hilft uns, die Anpassung des Modells an die Trainingsdaten zu beurteilen.
Schritt 5: Visualisierung der Testdaten
Ähnlich visualisieren wir die Testdaten, um die Modellleistung auf neuen, unsichtbaren Daten zu bewerten.
import matplotlib.pyplot as plt
# Visualisierung der Trainingsdaten
plt.scatter(X_train, y_train, color='green')
plt.plot(X_train, regressor.predict(X_train), color='blue')
plt.title('Personalkosten vs Psychopharmaka (Training set)')
plt.xlabel('Personalkosten im Jahr')
plt.ylabel('Psychopharmaka')
plt.show()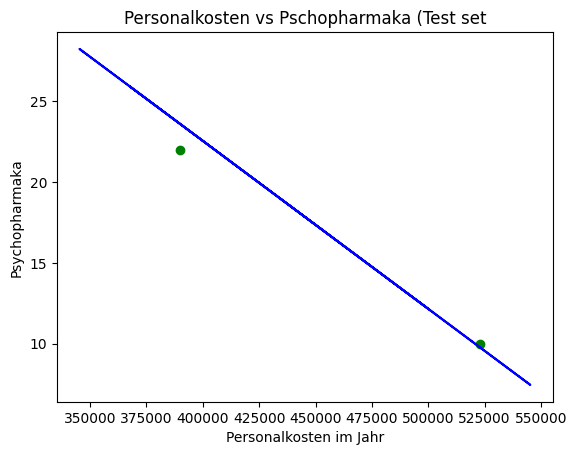
Erklärung: Das Streudiagramm der Testdaten zeigt, wie gut das Modell auf neuen Daten funktioniert. Die blauen Linie bleibt die gleiche, da sie auf den Trainingsdaten basiert.
Schritt 6: Vorhersage für neue Daten
Wir machen eine Vorhersage für neue Personalkosten.
# Vorhersage für die Personalkosten von 587000 Euro
print("Vorhersage für 587000 Euro Personalkosten:", regressor.predict([[587000]]))Erklärung: Wir verwenden das trainierte Modell, um die Anzahl der verordneten Psychopharmaka für neue Personalkosten von 587000 Euro vorherzusagen.
Schritt 7: Anzeigen der Modellparameter
Zum Schluss zeigen wir die Steigung und den Achsenabschnitt der Regressionslinie an.
# Anzeigen der Steigung und des Achsenabschnitts
print("Steigung (b1):", regressor.coef_)
print("Achsenabschnitt (b0):", regressor.intercept_)Erklärung: Die Steigung (b1) und der Achsenabschnitt (b0) definieren die lineare Gleichung
, die die Beziehung zwischen Personalkosten und der Anzahl der verordneten Psychopharmaka darstellt.
Fazit
Dieses Beispiel demonstriert die Anwendung einer einfachen linearen Regression, um die Beziehung zwischen Personalkosten und der Anzahl der verordneten Psychopharmaka in Pflegeheimen zu modellieren. Durch das Training und die Bewertung des Modells können wir wertvolle Einblicke gewinnen und fundierte Vorhersagen treffen.
Komplette Gleichung der linearen Regression
Psychopharmaka=64.06946364961881−0.00010383⋅Personalkosten




0 Kommentare